早速ですが質問です。

 

下記の台形の面積を求めてください。

 

 

 

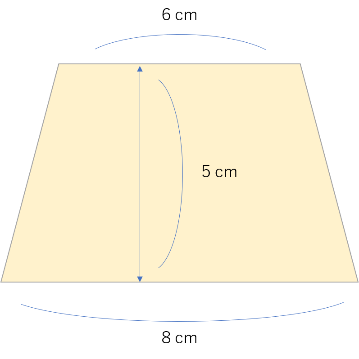
いかがですか？

 

 

この文章を読んでいる誰もが、小学生の頃に習っているはずです。

 

もし、

「なんだったっかな～、忘れた～」

と思われている人がいたとしたら、

おそらく台形の面積の求め方を、

 

{（上底＋下底）×高さ}÷２

 

という複雑な公式で覚えていた方でしょう。

 

テスト前日の一夜漬けならば、この方法で問題ありません。

しかし、人は忘れる生き物です。

 

数年後、数十年後でもいつでも思い出せるように、

公式そのものではなく、公式の導き方を知る方が良いのです。

 

例えば台形の面積の場合、

 

下記のように図形を二つ用意して、

逆転したものを横に付けます。

 

 

 

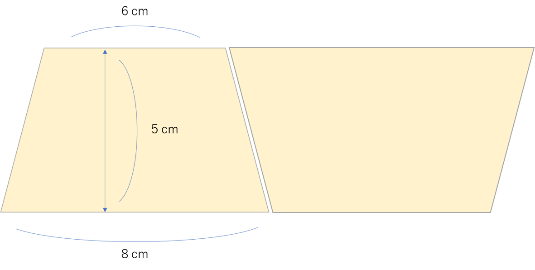
すると、ある図形になります。

 

覚えておりますか？

平行四辺形という図形ですね。

 

台形よりも面積を楽に求めることができます。

平行四辺形の面積を求める公式、覚えておりますか？

 

覚えていなくても大丈夫です。

公式を導き出すことができれば。

 

下記のように端をカットしてください。

そしてカットした部分を反転して、

もう片方の端にくっつけましょう。

 

 

すると、ただの長方形になりました！！

 

長方形の面積は大丈夫ですよね。

底辺×高さ、つまりこの場合は、

14cm×５cm＝70㎠です。

 

しかし、忘れてはいけません。

 

先程、図形を2つにしてくっつけました。

なので、2で割る必要があります。

 

ということで、

正解は70÷2で35㎠

でした。

 

改めて図形を見ると、

底辺は、上底＋下底だということが分かります。

それに高さを掛けて、2で割る。

 

この考え方であれば、

先程の一見複雑に見える公式を自分で導き出すことができます。

 

これは算数の話でしたが、

日常の仕事でも同じことが言えます。

 

例えば部下からの

「この場合、どのように対処したらよいですか？」

という質問に対して、答えを与えてしまうことが多いかもしれません。

 

しかし、答えを与えてしまうと、

次に同じようなことがあった場合、

その部下は、まるでロボットのように答えを引用するしかできないでしょう。

答えを忘れてしまうこともあります。

そして応用が全く効かない可能性もあります。

 

 

では、どうすればよいのか？

 

「どうすればよいと思う？」

と投げかけてみてください。

 

まずは本人に考えさせましょう。

 

自ら答えを導き出すことができれば、

忘れることはありません。

似たような事態があっても応用も効くでしょう。

 

また、自ら答えを導き出すことができなかった場合でも、

答えを教えたあとに、「理由」を必ず付け加えることが重要です。

 

 

一例として、

 

部下

「お客様が当社の製品に対して、デザインで気に入らない部分があり、

値引きを要求しています。どのように対処すればよいですか？」

 

上司

「どうすればよいと思う？」

 

部下

「デザインが気に入らないというのは、製品の落ち度でもあるので、

ある程度価格を下げることで要求を呑むべきかと…」

 

上司

「デザインは好みによる部分も多いよね。

それに当社は、デザインも含めて適正な対価として

金額を設定しているわけだから、値引きする必要はない。

デザイン以外の優位点をしっかり提案して、

それでも納得いただけなかったら仕方ないよ。

値引きはこちら側の商品やサービスに対する

明らかな落ち度があった場合だけだよ。」

 

こんなイメージです。

参考にして頂ければ幸いです。

 

後藤